Earlier this month Robert Kosara at
EagerEyes.org produced a visualisation of the difference, in historical US presidential elections, between the
popular vote and the Electoral College vote, cast by the delegates that the state voters actually elect to vote on their behalf. The questions this visualisation might answer include:
Q1 How big were the popular and EC votes?
Q2 How big was the difference?
Q3 How often and when was the popular vote greater than the EC vote?
Q4 Was the EC vote over 50% (a "majority"-- only a "plurality", i.e. more than anyone else, is necessary to actually win)?
Q5 Was the popular vote over 50% (sometimes called a "mandate")?
Q6 Were they on opposite sides of the 50% line?
Robert used a stacked bar graph, in order to show the answer to some of these questions. I'll use my own version of his graph for consistency, but the colours are the original ones:
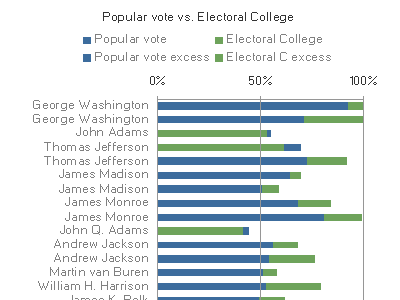
I found Q3 hard to compare across the years using Robert's graph, because detecting the difference meant seeing the change in position between the green and blue areas, and I had to do it consciously, instead of relying on
preattentive processing to bring the few instances to my attention.
Kelly O'Day suggested dot plots, with or without lines, but I found the differences in Q2 hard to compare across the years, and still the switch rounds in Q3 hard to detect. It seemed to me that the blue and green bars were interfering with each other, and strictly speaking were redundant anyway, so in comments I suggested removing them to make a "floating bar" graph.
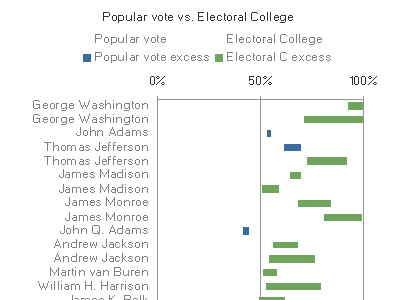
(In my original comment I changed the colours from blue and green to purple and teal, in an attempt to bring the hues round the colour circle toward the classic red-blue combination, without actually using red and blue, which for obvious reasons would be confusing in this political context. But I've decided the difference in hue discrimination wasn't dramatic enough to be worth the extra change)
Kelly liked it but said the scale didn't easily show the difference, which is true, but I was still trying to show the numbers in question Q1 as well as the difference in Q2. That purpose hadn't changed from the original bar graph, and I wouldn't want to just have a graph of the differences aligned along a common scale, because that would lose the Q1 information. I had only removed what I thought was duplicated information from the graph.
As a compromise, I present a re-colored stacked bar graph.
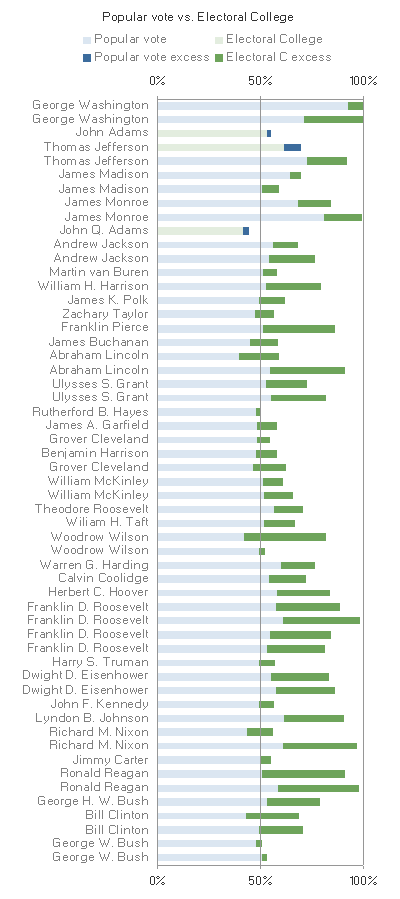
Now it's not floating any more, and there's no danger of interpreting it as a graph for differences only, but the eye is still drawn to the difference bars, and to the (three) instances where the popular vote is less than EC vote (Q3), and to the (seventeen) instances where the EC vote is a majority, but the popular vote isn't (Q6).
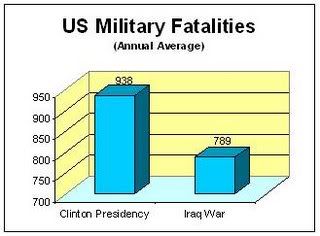
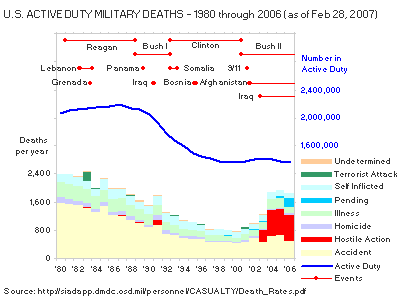
I've used this technique of more saturated colours to draw the eye, and lighter or less saturated ones to avoid distractions without removing information, in my blog post of a few months ago
Always show the distribution if you can. There, I wanted to emphasise Pentagon-reported military fatalities attributed to terrorist attack (dark green) and hostile action (red), without concealing all the rest of the data. It's all there, nothing hidden, but it isn't overwhelming the eye.









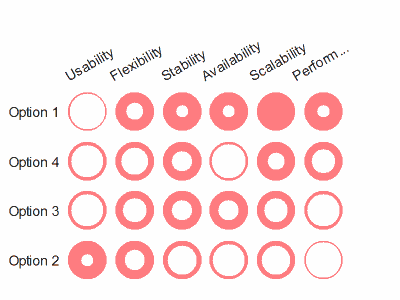
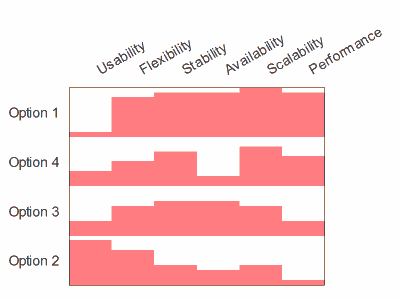
 Not very informative. So he tries it as a "petal chart"
Not very informative. So he tries it as a "petal chart"
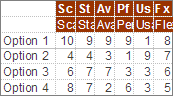


















 Where a distribution is highly right skewed, means and medians are far from the same. In the example I show on the right, the percentiles are as follows:
Where a distribution is highly right skewed, means and medians are far from the same. In the example I show on the right, the percentiles are as follows: